Circles

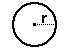
a circle

Definition: A circle is the locus of all points equidistant from a central point.

Definitions Related to Circles

arc: a curved line that is part of the circumference of a circle
chord: a line segment within a circle that touches 2 points on the circle.
circumference: the distance around the circle.
diameter: the longest distance from one end of a circle to the other.
origin: the center of the circle
pi ( $pi$ ): A number, 3.141592..., equal to (the circumference) / (the diameter) of any circle.
radius: distance from center of circle to any point on it.
sector: is like a slice of pie (a circle wedge).
tangent of circle: a line perpendicular to the radius that touches ONLY one point on the circle.

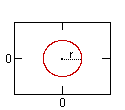
diameter = 2 x radius of circle

Circumference of Circle = PI x diameter = 2 PI x radius
where PI = $PI$ = 3.141592...

Area of Circle:
area = PI r²

Length of a Circular Arc: (with central angle $theta$ )
if the angle $theta$ is in degrees, then length = $theta$ x (PI/180) x r
if the angle $theta$ is in radians, then length = r x $theta$

Area of Circle Sector: (with central angle $theta$ )
if the angle $theta$ is in degrees, then area = ( $theta$ /360) PI r²
if the angle $theta$ is in radians, then area = ( $theta$ /2) r²

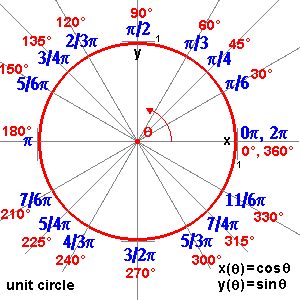
Equation of Circle: (cartesian coordinates)
$graph circle$
for a circle with center (j, k) and radius (r):
(x-j)² + (y-k)² = r²

Equation of Circle: (polar coordinates)
for a circle with center (0, 0): r( $theta$ ) = radius

for a circle with center with polar coordinates: (c, $alpha$ ) and radius a:
r² - 2cr cos( $theta$ - $alpha$ ) + c² = a²

Equation of a Circle: (parametric coordinates)
for a circle with origin (j, k) and radius r:
x(t) = r cos(t) + j y(t) = r sin(t) + k

$parametric unit circle$