Quadrilaterals (sparknotes/reference)

Quadrilaterals

Quadrilaterals are prevalent shapes in the world, and thus have been classified carefully. The four sides of quadrilaterals naturally come in pairs, with opposite sides being those that don't share a vertex. Many quadrilaterals have pairs of opposite sides with no special relationships, but then again, some do.

Parallelograms

A parallelogram is a quadrilateral whose opposite sides are parallel. Below a few parallelograms are pictured.

Figure 4.1: Some parallelograms

A parallelogram has many interesting properties. Its opposite sides, in addition to being parallel, are congruent. The opposite angles of a parallelogram are also congruent. Consecutive angles of a parallelogram, are supplementary. Also, the diagonals of a parallelogram bisect each other. These properties are pictured below.

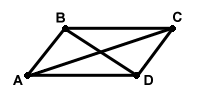
Figure 4.2: Properties of a parallelogram

In the above picture, AB=CD and AD=BC. Angles ABC and ADC are congruent, as are angles BCD and BAD. Every pair of consecutive angles, like angle ABC and BCD for example, are supplementary. Also, the diagonals AC and BD bisect each other.

Parallelograms can be broken down into different categories as well. Parallelograms with four congruent sides are called rhombuses. Parallelograms with four right angles are called rectangles. And a parallelogram whose sides and angles are all congruent is a square.

Figure 4.3: A rhombus, rectangle, and square

Trapezoids

A quadrilateral with only one pair of parallel sides is called a trapezoid. Here some trapezoids are pictured.

Figure 4.4: Some trapezoids

The parallel sides of a trapezoid are called the bases of the trapezoid. A trapezoid's nonparallel sides are its legs. One of the most important parts of a trapezoid is its median. The median of a trapezoid is the segment that joins the midpoints of the legs of the trapezoid. It is parallel to the bases, and is equal to half the sum of the length of the bases; its length is the average length of the bases.

Figure 4.5: A trapezoid and its median

These special quadrilaterals are helpful because they can be used as estimates of real-life four-sided shapes, and their properties make calculations easy.