

A triangle is a 3-sided polygon sometimes (but not very commonly) called the trigon. Every triangle has three sides and three angles, some of which may be
the same. The sides of a triangle are given special names in the case of a right triangle, with the side opposite the right angle being termed the hypotenuse and the other two sides being known as the legs. All triangles are convex and bicentric. That portion of the plane enclosed by the triangle is called the triangle interior, while the remainder is the exterior.
The study of triangles is sometimes known as triangle geometry, and is a rich area of geometry filled with beautiful results and unexpected connections. In 1816, while studying the Brocard points of a triangle, Crelle exclaimed, "It is indeed wonderful that so simple a figure as the triangle is so inexhaustible in properties.
How many as yet unknown properties of other figures may there not be?" (Wells 1991, p. 21).
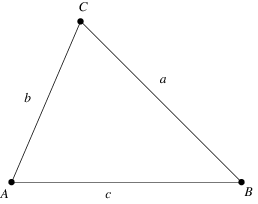 It is common to label the vertices of a triangle in counterclockwise order as either 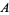 , , 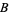 , , 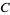 (or (or 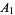 , , 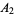 , , 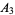 ). The vertex angles are then given the same symbols as the vertices themselves. The symbols ). The vertex angles are then given the same symbols as the vertices themselves. The symbols 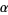 , , 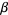 , , 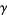 (or (or 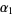 , , 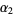 , , 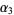 ) are also sometimes used (e.g., Johnson 1929), but this convention results in unnecessary confusion with the common notation
for trilinear coordinates ) are also sometimes used (e.g., Johnson 1929), but this convention results in unnecessary confusion with the common notation
for trilinear coordinates 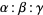 , and so is not recommended. The sides opposite the angles , and so is not recommended. The sides opposite the angles 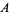 , , 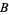 , and , and 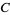 (or (or 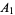 , , 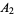 , , 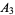 ) are then labeled ) are then labeled 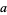 , , 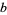 , , 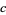 (or (or 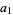 , , 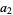 , , 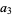 ), with these symbols also indicating the lengths of the sides (just as the symbols at the vertices indicate the vertices
themselves as well as the vertex angles, depending on context). ), with these symbols also indicating the lengths of the sides (just as the symbols at the vertices indicate the vertices
themselves as well as the vertex angles, depending on context).
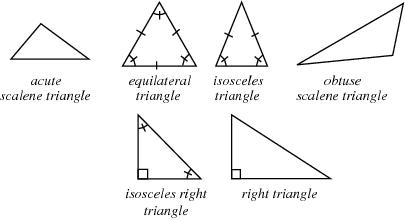 An triangle is said to be acute if all three of its angles are all acute, a triangle having an obtuse angle is called an obtuse triangle, and a triangle with a right angle is called right. A triangle with all sides equal is called equilateral, a triangle with two sides equal is called isosceles, and a triangle with all sides a different length is called scalene. A triangle can be simultaneously right and isosceles, in which case it is known as an isosceles right triangle.
The semiperimeter 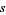 of a triangle is defined as half its perimeter, of a triangle is defined as half its perimeter,
The area of a triangle can given by Heron's formula
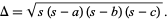 |
(3) |
There are also many other formulas for the triangle area.
The definition of the semiperimeter leads to the definitions
where 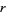 is the inradius. A similar set of relations hold for Conway triangle notation is the inradius. A similar set of relations hold for Conway triangle notation 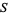 , , 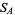 , , 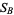 , and , and 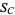 . .
The sum of angles in a triangle is 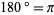 radians (at least in Euclidean geometry; this statement does not hold in non-Euclidean geometry). This can be established as follows. Let radians (at least in Euclidean geometry; this statement does not hold in non-Euclidean geometry). This can be established as follows. Let 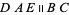 ( (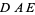 be parallel to be parallel to 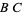 ) in the above diagram, then the angles ) in the above diagram, then the angles 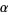 and and 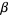 satisfy satisfy
|

