A plane is a boundless surface in space. It has length, like a line; it also has width, but not thickness. A plane is denoted by writing "plane P", or just writing "P". On paper, a plane looks something like this:

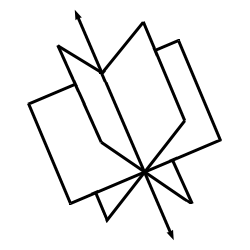
There are two ways to form a plane. First, a plane can be formed by three noncolinear points. Any number of colinear points form one line, but such a line can lie in an infinite number of distinct planes. See below how different planes can contain the same line. It takes a third, noncolinear point to form a specific plane. This point fixes the plane in position. The situation is something like a door being shut. Before the door is shut, it swings on hinges, which form a line. The door (a plane) can be opened to an infinite number of different positions, maybe just cracked a few inches, or maybe wide open (figures a, b in the diagram below). When the door is shut however, the wall on the other side of the hinges acts as the noncolinear third point and holds the door in place. At this point, the door represents one distinct plane (figure c).

The second way to form a plane is with a line and a point in that line. There are just two conditions. 1) the line must be perpendicular to the plane being formed (for an explanation of this concept, see Geometric Surfaces, Lines and Planes); 2) the point in the line must also be in the plane being formed. Given a line, a point in that line, and these conditions, a plane is determined.

When points lie in the same plane, they are called coplanar. When points lie in different planes, they are called noncoplanar. The concept is much like that of colinearity.

As previously mentioned, a plane has no thickness. Remember that though the diagrams shown here make it appear otherwise, a plane also has no limits: it is an endless surface in space. Most of the geometry you will see in this guide will deal with plane geometry. We will deal with "flat" shapes that lie in a plane, and therefore have no thickness. All of the points in such geometric figures are coplanar.